2005 年の東大文系の問題を小学生レベルに改題できることに気づきました。
3 以上 9999 以下の奇数
で,
が 10,000 で割り切れるものをすべて求めよ。
途中式の桁数を与えると虫食い算に直せます。
次の式をみたす奇数
を求めなさい。
〜
に同じ数字を使ってもよいこととします。
簡単に解き方を解説しましょう。 の下一桁が
であることから
の候補は 1, 5, 6。
は奇数なので 6 は不適。
が 4 桁の数であることから 1 も不適で,
がわかります。
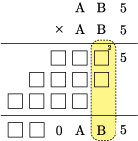
図の枠内の計算では「繰り上がりの 2」「 の一の位」「
の一の位」の和の一の位が
になります。
が 2 つあるのは
と同じで,これの一の位は 0 なので
と決まります。
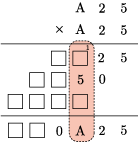
もう一度同じことをやると もわかってできあがりです。
