正12角形の面積を求める問題をやりました。
問題1 1辺の長さが1の正12角形の面積を求めよ。
外接円を描き,その中心と各頂点を結び……とやりたくなるところですが,実は正方形と正三角形に分割できます。三角関数は使いません。

よくこんなの思いつくものだと思ったら,案の定,元ネタがありました。ガードナーの本に載ってます。
マルクウィッチ(Joseph Malkwitch)が1968年に出題し,ゴールドバーグ(Micheal Goldberg)が American Mathematical Monthly 誌1969年5月号に解答を寄せたそうです。
問題2 一辺の長さが同一単位の正方形と正三角形のボール紙が限りなく手に入るものと仮定する。それらを使って3辺から10辺までの凸多角形を作るのは簡単である。では11の辺からなる凸多角形を作ることはできるだろうか? また,そのようなボール紙で作れる凸多角形の辺の個数の最大値はいくつか?
3角形~10角形については図が載っていました。

類題が広中杯トライアルと麻布中で出題されています。
問題3(2000 広中杯トライアル) 1辺の長さが 1 cm の正三角形と正方形がたくさんあります。いま,これらをすきまなく置いて最小の凸11角形(へこみのない11角形)を作るとき,次の問に答えなさい。
(1) できた凸11角形の周の長さを求めなさい。
(2) この凸11角形を作るのに使った正三角形と正方形の個数をそれぞれ求めなさい。
問題4(1995 麻布中) 1辺の長さが 1 cm の正三角形と正方形がたくさんあります。それらを2個以上並べて,1辺が 1 cm の正多角形を作ります。そのとき,それらが互いに重ならないように,また,すき間がないように並べます。このとき次の問いに答えなさい。(図をかくとき,定規,コンパスは使わなくてもよい。)
(1) 正三角形または正方形のうち1種類だけで作る場合,できあがった正多角形の図を並べ方がわかるようにかきなさい。
(2) 正三角形と正方形の2種類で作る場合
(イ) できあがった正多角形の1つの角は何度ですか。
(ロ) できあがった正多角形の図を並べ方がわかるようにかきなさい。
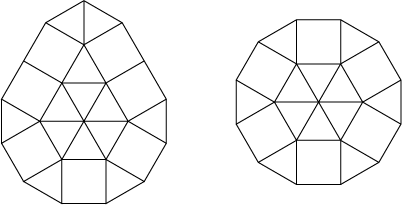
麻布の正12角形はともかく,広中杯の11角形は思いつきにくいです。解法は下の本に載っているので,気になる人はどうぞ。
麻布の問題の解答も赤本をどうぞ。下の本に載っているのと同じ考え方で正多角形は3,4,6,12角形しか作れないことが証明できます。


